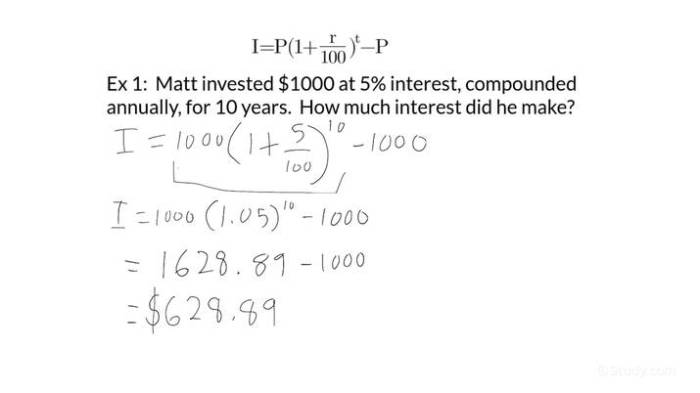
Navigating the complexities of student loan repayment often leaves borrowers questioning the intricacies of interest accrual. Understanding whether your student loan interest is compounded, and how this compounding works, is crucial for effective financial planning and minimizing long-term costs. This exploration delves into the mechanics of compound interest as it applies to student loans, offering clarity on its impact and strategies for managing its effects.
This article will dissect the process of compound interest calculation, comparing it to simple interest to highlight the significant differences in total repayment. We will examine how various factors, such as interest rates, loan amounts, and repayment plans, influence the final cost. Finally, we’ll provide practical strategies to help you minimize the impact of compound interest on your overall student loan debt.
Understanding Compound Interest in the Context of Student Loans
Compound interest is a crucial concept to grasp when dealing with student loans, as it significantly impacts the total amount you’ll repay. Unlike simple interest, which is calculated only on the principal loan amount, compound interest is calculated on the principal amount plus any accumulated interest. This means your debt grows exponentially over time. Understanding how this works is key to responsible loan management.
Compound Interest Calculation on Student Loans
Compound interest calculations involve determining the interest accrued on the principal amount and adding it to the principal, then calculating the interest on the new, larger amount in subsequent periods. The formula for compound interest is: A = P (1 + r/n)^(nt), where: A = the future value of the investment/loan, including interest; P = the principal investment amount (the initial deposit or loan amount); r = the annual interest rate (decimal); n = the number of times that interest is compounded per year; and t = the number of years the money is invested or borrowed for.
Step-by-Step Example: $10,000 Loan at 5% Interest Over 10 Years
Let’s illustrate with a $10,000 loan at a 5% annual interest rate compounded annually over 10 years.
Step 1: Identify the variables. P = $10,000; r = 0.05; n = 1 (compounded annually); t = 10.
Step 2: Apply the formula: A = 10000 (1 + 0.05/1)^(1*10) = 10000 (1.05)^10 ≈ $16,288.95
Step 3: The total interest paid is approximately $16,288.95 – $10,000 = $6,288.95. This demonstrates the significant impact of compounding over time.
Simple Interest Versus Compound Interest: A Comparison
Simple interest is calculated only on the principal amount. In contrast, compound interest is calculated on the principal plus accumulated interest. This difference leads to substantially higher repayment amounts under compound interest. For example, using the same $10,000 loan at 5% interest over 10 years, simple interest would result in a total repayment of $15,000 ($10,000 principal + $5,000 interest). The difference between the simple interest repayment ($15,000) and the compound interest repayment ($16,288.95) highlights the power of compounding.
Loan Repayment Schedules Under Simple and Compound Interest
| Loan Amount | Interest Rate | Simple Interest Repayment | Compound Interest Repayment |
|---|---|---|---|
| $10,000 | 5% | $15,000 | $16,288.95 |
| $20,000 | 6% | $32,000 | $35,816.95 (approximately, assuming annual compounding) |
| $5,000 | 4% | $7,000 | $7,289.05 (approximately, assuming annual compounding) |
| $15,000 | 7% | $25,500 | $28,677.47 (approximately, assuming annual compounding) |
Factors Affecting Compound Interest on Student Loans
Understanding the factors that influence the growth of compound interest on student loans is crucial for effective financial planning. The total amount you’ll repay significantly depends on several interconnected variables, impacting your overall financial health. Careful consideration of these factors can help borrowers make informed decisions and potentially save thousands of dollars over the life of their loans.
Several key factors determine the amount of compound interest accrued on your student loans. These factors interact in complex ways, so understanding their individual and collective effects is essential for responsible loan management.
Interest Rate
The interest rate is the percentage of your loan balance charged as interest each year. A higher interest rate leads to faster compound interest growth, resulting in a larger total repayment amount. For example, a loan with a 7% interest rate will accrue significantly more interest over time than a loan with a 4% interest rate, even if the principal amounts are the same. The interest rate is usually fixed for the life of the loan, but some loans offer variable rates, which can fluctuate over time, adding complexity to repayment projections.
Loan Amount
The principal loan amount—the initial sum borrowed—directly impacts the amount of compound interest accrued. A larger loan balance means more interest is calculated each period, leading to a larger total interest payment over the life of the loan. A $50,000 loan will generate considerably more interest than a $20,000 loan, assuming all other factors remain constant.
Repayment Plan
Different repayment plans affect the total compound interest paid. A standard repayment plan typically involves fixed monthly payments over a set period (e.g., 10 years). Graduated repayment plans start with lower payments that gradually increase over time. Income-driven repayment plans base monthly payments on your income and family size, potentially extending the repayment period significantly. Longer repayment periods, as seen in income-driven plans, generally result in higher total interest paid due to the longer accumulation period. Conversely, shorter repayment periods, like those in standard plans, reduce the overall interest paid, though the monthly payments are higher.
Capitalization
Capitalization occurs when accrued interest is added to the principal loan balance. This increases the principal amount on which future interest is calculated, accelerating the growth of compound interest. For example, if interest is capitalized annually, the interest accrued during the first year is added to the principal balance at the beginning of the second year. Subsequently, interest is calculated on this larger amount, leading to a snowball effect. Loans with frequent capitalization periods will accrue interest more rapidly than loans with less frequent or no capitalization.
Strategies for Minimizing Compound Interest on Student Loans
Understanding the mechanics of compound interest is vital for minimizing its impact. Here are some key strategies:
- Choose a shorter repayment plan: Shorter repayment periods, even with higher monthly payments, result in less total interest paid.
- Make extra payments: Paying more than the minimum payment each month reduces the principal balance faster, leading to less interest accrued over time.
- Refinance your loans: If interest rates have fallen since you took out your loans, refinancing to a lower interest rate can significantly reduce your overall interest payments.
- Explore income-driven repayment plans: While these plans extend the repayment period, they may offer lower monthly payments, making them manageable during periods of lower income.
- Consolidate your loans: Consolidating multiple loans into a single loan can simplify repayment and potentially lower your interest rate.
The Impact of Different Interest Rates and Loan Terms

Understanding the interplay between interest rates and loan terms is crucial for minimizing the overall cost of your student loans. Small variations in these factors can lead to substantial differences in the total amount repaid over the life of the loan. This section will explore how different interest rates and repayment periods affect the total interest paid and the overall cost of a loan.
The total interest paid on a student loan is directly influenced by both the interest rate and the loan term. A higher interest rate will naturally result in a larger amount of interest accruing over time. Similarly, a longer repayment term, while resulting in lower monthly payments, allows more time for interest to accumulate, increasing the total amount paid. Conversely, shorter loan terms lead to higher monthly payments but significantly reduce the overall interest paid.
Interest Rate Comparison: 4% vs. 7%
Let’s compare two $20,000 loans, one with a 4% interest rate and another with a 7% interest rate, both over a 10-year repayment period. Using a standard amortization calculator (readily available online), we can see a significant difference. The 4% loan would result in approximately $2,910 in total interest paid, while the 7% loan would accumulate approximately $6,000 in interest. This illustrates how a seemingly small difference of 3% in interest rates can lead to a substantial increase in the total cost of the loan.
The Effect of Loan Repayment Term
Extending or shortening the loan repayment term has a significant impact on the total interest paid. A longer repayment term, while reducing monthly payments, allows interest to compound over a longer period, resulting in a substantially higher total interest paid. Conversely, a shorter repayment term, although resulting in higher monthly payments, significantly reduces the total interest paid. For example, a $20,000 loan at 6% interest would accrue approximately $7,610 in interest over 10 years, $13,370 over 15 years, and $19,130 over 20 years.
Total Loan Cost with Varying Interest Rates and Repayment Terms
The following table illustrates the total cost of a $20,000 loan under various interest rate and repayment term scenarios:
| Interest Rate | Repayment Term (Years) | Total Interest Paid | Total Repayment Amount |
|---|---|---|---|
| 4% | 10 | $2,910 (approx.) | $22,910 |
| 4% | 15 | $4,360 (approx.) | $24,360 |
| 4% | 20 | $5,820 (approx.) | $25,820 |
| 5% | 10 | $3,660 (approx.) | $23,660 |
| 5% | 15 | $5,620 (approx.) | $25,620 |
| 5% | 20 | $7,580 (approx.) | $27,580 |
| 6% | 10 | $4,410 (approx.) | $24,410 |
| 6% | 15 | $6,870 (approx.) | $26,870 |
| 6% | 20 | $9,130 (approx.) | $29,130 |
| 7% | 10 | $6,000 (approx.) | $26,000 |
| 7% | 15 | $8,920 (approx.) | $28,920 |
| 7% | 20 | $11,800 (approx.) | $31,800 |
Note: These figures are approximate and may vary slightly depending on the specific amortization calculation method used.
The Significance of Small Interest Rate Differences
Even seemingly insignificant differences in interest rates can have a dramatic impact on the total cost of a student loan over its lifetime. The compounding effect of interest means that small increases in the interest rate lead to exponentially larger increases in the total interest paid over the loan’s duration. Careful consideration of interest rates and repayment terms is essential for responsible financial planning.
Visual Representation of Compound Interest Growth
Understanding the exponential growth of student loan debt due to compound interest is best achieved through visual aids. A graph provides a clear and intuitive representation of how your loan balance increases over time, highlighting the accelerating effect of compounding.
A graph illustrating compound interest on a student loan typically displays time on the x-axis and the loan balance on the y-axis. The line representing the loan balance won’t be straight; instead, it will curve upwards, demonstrating exponential growth. The steeper the curve becomes over time, the more rapidly the loan balance is increasing due to the accumulating interest. Initially, the increase in the loan balance might appear modest, but as time passes and interest compounds on both the principal and accumulated interest, the growth accelerates dramatically. This visual representation powerfully illustrates how even small interest rates can significantly impact the total amount owed over the life of the loan.
Graph of Student Loan Balance Over Time
Imagine a graph with the horizontal axis (x-axis) representing the time elapsed since the loan was taken out, measured in years. The vertical axis (y-axis) represents the total loan balance, including both principal and accumulated interest. The graph would start at a point representing the initial loan amount. As time progresses, the line representing the loan balance would curve upwards, initially gently, but then increasingly steeply. This upward curve vividly portrays the effect of compound interest—the interest earned on previously accumulated interest, causing the loan balance to grow at an accelerating rate. Points along the line would represent the loan balance at specific time intervals, clearly showing the growth over time. For instance, a point at year 5 would indicate the total balance after five years, including the principal and all compounded interest.
Visualizing the Impact of Early Repayment
To illustrate the benefits of early repayment, we can compare two graphs. The first graph would show the growth of a student loan balance without any extra payments, mirroring the scenario described above. The second graph would represent the same loan but with consistent early repayments made throughout the loan term. This second graph would show a significantly flatter curve compared to the first. The difference between the two curves visually represents the total amount of interest saved by making early repayments. The earlier the repayments start, the more pronounced this difference will be, demonstrating how proactive repayment strategies can dramatically reduce the overall cost of borrowing. The area between the two curves represents the monetary savings achieved through early repayment. This area will be considerably larger if early repayments begin sooner in the loan term, further emphasizing the advantages of prompt repayment.
Closure
In conclusion, understanding the compounding nature of student loan interest is paramount to responsible debt management. While the exponential growth of compound interest can seem daunting, proactive strategies like choosing favorable repayment plans, making extra payments, and refinancing when appropriate can significantly reduce the overall cost of your loan. By actively engaging with your loan details and employing smart repayment strategies, you can navigate the complexities of student loan debt and achieve financial freedom sooner.
Essential Questionnaire
What happens if I miss a student loan payment?
Missing payments can lead to late fees, negatively impacting your credit score and potentially triggering loan default. It also increases the total interest paid due to compounding.
Can I refinance my student loans to lower my interest rate?
Yes, refinancing can potentially lower your interest rate, leading to lower monthly payments and reduced overall interest paid. However, it’s important to compare offers carefully and consider the terms and conditions before refinancing.
What is capitalization in the context of student loans?
Capitalization occurs when unpaid interest is added to your principal loan balance, increasing the amount on which future interest is calculated. This accelerates the growth of your debt.
Are there any government programs to help with student loan repayment?
Yes, various government programs offer income-driven repayment plans and potential loan forgiveness options depending on your employment and other factors. Research programs like Income-Driven Repayment (IDR) plans.
