
Navigating the complexities of student loan repayment can feel daunting, but understanding your amortization schedule is key to financial freedom. This guide provides a comprehensive overview of student loan amortization tables, explaining their components and demonstrating how to create one using Microsoft Excel. We’ll explore various scenarios, including different interest rates and loan terms, to empower you with the knowledge to make informed decisions about your debt repayment strategy.
From understanding the fundamental concepts of principal, interest, and payment calculations to mastering Excel functions like PMT, IPMT, and PPMT, this guide will equip you with the tools to build your own personalized amortization table. We’ll also delve into advanced features, such as incorporating extra payments and adjusting for interest rate changes, providing a holistic approach to managing your student loan debt effectively.
Understanding Amortization Tables
Amortization tables are crucial tools for understanding how student loans are repaid over time. They break down each payment into its principal and interest components, providing a clear picture of how the loan balance decreases with each payment. This detailed breakdown allows borrowers to track their progress and understand the overall cost of their loan.
Amortization tables typically display several key components.
Amortization Table Components
An amortization table displays the following information for each payment period (usually monthly): The principal represents the original loan amount borrowed. The interest is the cost of borrowing money, calculated as a percentage of the remaining balance. The payment amount is the fixed amount paid each period. Finally, the remaining balance shows the amount still owed after each payment. These components work together to illustrate the repayment process.
Amortization Table Calculations
Calculating the monthly payment on a student loan involves a formula that considers the loan amount, interest rate, and loan term. The most common method uses the following formula:
M = P [ i(1 + i)^n ] / [ (1 + i)^n – 1]
Where:
* M = Monthly payment
* P = Principal loan amount
* i = Monthly interest rate (Annual interest rate divided by 12)
* n = Total number of payments (Loan term in years multiplied by 12)
The amortization table then uses this calculated monthly payment to determine the allocation between principal and interest for each payment. In the early stages of repayment, a larger portion of the payment goes towards interest, while the proportion allocated to principal increases over time.
Amortization Schedules: Fixed vs. Variable Rates
Student loans can have either fixed or variable interest rates. A fixed-rate loan maintains a consistent interest rate throughout the loan term, making repayment predictable. A variable-rate loan, on the other hand, has an interest rate that fluctuates based on market conditions. This can lead to unpredictable monthly payments and a potentially longer repayment period if rates rise. An amortization table for a variable-rate loan will reflect these changes in the interest portion of each payment, leading to variations in the remaining balance compared to a fixed-rate loan.
Example Amortization Table
Below is a simplified amortization table showing the first five months of repayment for a $10,000 loan at a 5% annual interest rate over 10 years. Note that these figures are approximate and do not include any potential fees.
| Month | Payment | Principal | Interest | Balance |
|---|---|---|---|---|
| 1 | $106.07 | $41.67 | $64.40 | $9958.33 |
| 2 | $106.07 | $42.08 | $63.99 | $9916.25 |
| 3 | $106.07 | $42.49 | $63.58 | $9873.76 |
| 4 | $106.07 | $42.90 | $63.17 | $9830.86 |
| 5 | $106.07 | $43.32 | $62.75 | $9787.54 |
Building an Amortization Table in Excel

Creating an amortization schedule in Excel provides a clear and detailed breakdown of your loan repayment, showing the principal and interest components of each payment over the loan’s life. This allows for a comprehensive understanding of your loan’s financial implications. This process leverages several built-in Excel functions.
Excel offers several powerful functions specifically designed for loan amortization calculations. Understanding these functions is key to building an accurate and informative amortization table.
Excel Functions for Amortization
The core functions used in building an amortization table are PMT, IPMT, and PPMT. These functions, when used correctly, will generate the necessary data for a comprehensive amortization schedule.
- PMT (Payment): This function calculates the total periodic payment for a loan. The syntax is
PMT(rate, nper, pv, [fv], [type])where ‘rate’ is the periodic interest rate, ‘nper’ is the total number of payment periods, ‘pv’ is the present value (loan amount), ‘fv’ is the future value (optional, defaults to 0), and ‘type’ specifies when payments are due (0 for end of period, 1 for beginning, defaults to 0). - IPMT (Interest Payment): This function calculates the interest portion of a specific payment. The syntax is
IPMT(rate, per, nper, pv, [fv], [type])where ‘per’ represents the period for which you’re calculating the interest payment. - PPMT (Principal Payment): This function calculates the principal portion of a specific payment. The syntax is
PPMT(rate, per, nper, pv, [fv], [type]), similar to IPMT, with ‘per’ indicating the payment period.
Building an Amortization Table: A Step-by-Step Guide
Let’s construct an amortization table for a $20,000 loan at 7% annual interest over 5 years (60 months).
First, set up your spreadsheet. In cell A1, enter “Month”. In cell B1, enter “Beginning Balance”. In cell C1, enter “Payment”. In cell D1, enter “Interest Paid”. In cell E1, enter “Principal Paid”. In cell F1, enter “Ending Balance”.
Next, input the loan details. In a separate area (e.g., cells H1:H4), enter the following: In H1, “Loan Amount:”, H2, 20000; In H3, “Annual Interest Rate:”, H4, 0.07; In H5, “Loan Term (Years):”, H6, 5.
Now, calculate the monthly interest rate. In cell H7, enter the formula =H4/12. This divides the annual interest rate by 12 to get the monthly rate.
Calculate the number of payments. In cell H8, enter the formula =H6*12. This multiplies the loan term (in years) by 12 to get the total number of payments.
Calculate the monthly payment. In cell H9, enter the formula =PMT(H7,H8,H2). This uses the PMT function to calculate the monthly payment. The result will be a negative number because it represents an outflow of cash.
Now, let’s populate the amortization table. In cell A2, enter “1”. In cell B2, enter =H2 (the initial loan amount). In cell C2, enter =H9 (the monthly payment calculated above). In cell D2, enter =IPMT(H7,1,H8,H2). In cell E2, enter =PPMT(H7,1,H8,H2). In cell F2, enter =B2-E2.
For subsequent months (rows 3 and below), you will use relative and absolute cell references to continue the calculation. For example:
In cell A3, enter “2”. In cell B3, enter =F2 (the ending balance from the previous month). In cell C3, enter =H9 (the monthly payment). In cell D3, enter =IPMT($H$7,A3,$H$8,$B$3) (Note the use of absolute references for the interest rate, number of payments and beginning balance). In cell E3, enter =PPMT($H$7,A3,$H$8,$B$3) (similar absolute references here). In cell F3, enter =B3-E3.
Copy the formulas from row 3 down to row 61 to complete the amortization table. You should now have a complete amortization schedule showing the monthly payments, interest paid, principal paid, and ending balance for each month of the loan. Remember that the interest and principal paid will change each month. The beginning balance for each month is the ending balance from the previous month. The ending balance should approach zero by the end of the loan term.
Analyzing Amortization Schedules
Understanding an amortization schedule allows for a thorough examination of loan repayment, revealing crucial insights into the financial implications of different loan structures. By analyzing various scenarios, borrowers can make informed decisions that align with their financial capabilities and long-term goals.
Interest Rate Impact on Total Interest Paid
Let’s consider a hypothetical $20,000 student loan with a 10-year repayment term. We’ll compare the total interest paid under two different interest rates: 5% and 7%. An amortization table for the 5% loan would show a significantly lower total interest paid compared to the 7% loan. The higher interest rate dramatically increases the cumulative interest expense over the life of the loan. For example, the 5% loan might accrue around $3,000 in interest, while the 7% loan could accrue closer to $5,000. This difference highlights the importance of securing the lowest possible interest rate.
Loan Term Length’s Effect on Monthly Payments and Total Interest
The length of the loan term significantly impacts both monthly payments and the total interest paid. A shorter loan term, such as a 5-year repayment plan for our $20,000 loan, will result in higher monthly payments but substantially lower total interest paid over the life of the loan. Conversely, a longer loan term, such as a 20-year plan, will lead to lower monthly payments but a significantly higher total interest paid due to the extended repayment period. This trade-off between affordability and overall cost is a key consideration for borrowers.
Key Factors Influencing Student Loan Costs
Several key factors influence the overall cost of a student loan. These include the principal loan amount (the initial borrowed amount), the interest rate, the loan term length, and any applicable fees. A higher principal loan amount naturally increases the total cost. The interest rate, as discussed earlier, is a major determinant of total interest paid. Longer loan terms increase the total interest paid, while fees add directly to the overall cost. Understanding the interplay of these factors is essential for responsible borrowing.
Advantages and Disadvantages of Different Repayment Plans
Different repayment plans offer varying advantages and disadvantages. A standard repayment plan provides fixed monthly payments over a set period (typically 10 years), offering predictability but potentially higher monthly payments. Extended repayment plans lengthen the repayment period, resulting in lower monthly payments but significantly higher total interest paid. Income-driven repayment plans tie monthly payments to a borrower’s income, offering flexibility but potentially extending the repayment period significantly and potentially leading to higher overall interest costs. The best plan depends on individual financial circumstances and priorities.
Advanced Amortization Table Features
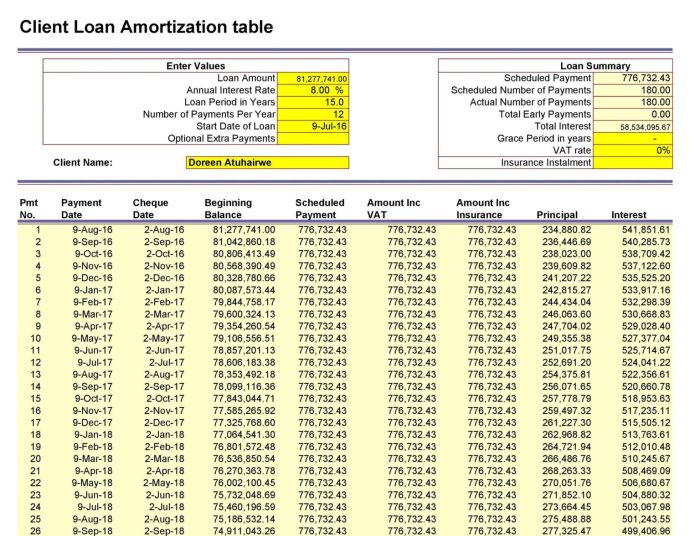
Building upon a basic amortization schedule, we can enhance its functionality to model more realistic loan repayment scenarios. This involves incorporating factors like extra payments and fluctuating interest rates, providing a more comprehensive understanding of loan repayment.
Incorporating Extra Payments
Adding extra payments to your amortization table significantly impacts the loan’s repayment timeline and overall interest paid. To implement this in Excel, you’ll need an additional column representing extra payments made in each period. This column should be added to the regular payment column for that period’s calculation. The principal reduction will increase, shortening the loan’s term. For instance, consider a $200,000 loan with a 6% interest rate amortized over 30 years. Adding an extra $200 per month would reduce the loan’s total repayment period by approximately 5 years and save thousands in interest. The formula for the remaining balance would need to adjust to account for these extra payments. The visual representation would show a steeper decline in the principal balance over time compared to a schedule without extra payments.
Adjusting for Interest Rate Changes
Interest rate fluctuations are common, and an amortization table should reflect these changes. To incorporate this, you can use a formula that references a cell containing the current interest rate. This cell can be updated as the interest rate changes. The amortization schedule will recalculate automatically, demonstrating the impact on the monthly payment and the total interest paid. For example, an increase in the interest rate will result in a higher monthly payment and a longer repayment period or a higher total interest paid if the payment remains the same. Conversely, a decrease will have the opposite effect. A visual representation would show two lines: one for the original interest rate and another showing the impact of the change. The steeper line would represent the higher interest rate.
Visual Representation of Varying Payment Amounts
The impact of different payment amounts on the amortization schedule can be visualized by creating multiple amortization tables, each with a different payment amount. For instance, you could create three tables: one with the minimum payment, one with a slightly higher payment, and one with a significantly higher payment. Comparing these tables visually demonstrates how increasing the payment amount drastically reduces the loan’s repayment period and total interest paid. The visual representation would show three lines depicting the principal balance over time. The line representing the highest payment amount would decline the fastest.
Calculating the Remaining Balance
Determining the remaining loan balance at any given point is crucial. This can be easily done by referencing the “Ending Balance” column in your amortization table for the corresponding period. Alternatively, a formula can be created to calculate this balance directly, based on the loan’s initial amount, interest rate, payment amount, and the number of payments made. This formula, based on the standard loan amortization formula, allows for calculating the remaining balance without needing the full amortization table. For example,
Remaining Balance = PV * (1 + r)^n – PMT * [((1 + r)^n – 1) / r]
where PV is the present value (initial loan amount), r is the periodic interest rate, n is the number of periods remaining, and PMT is the periodic payment.
Practical Applications and Considerations
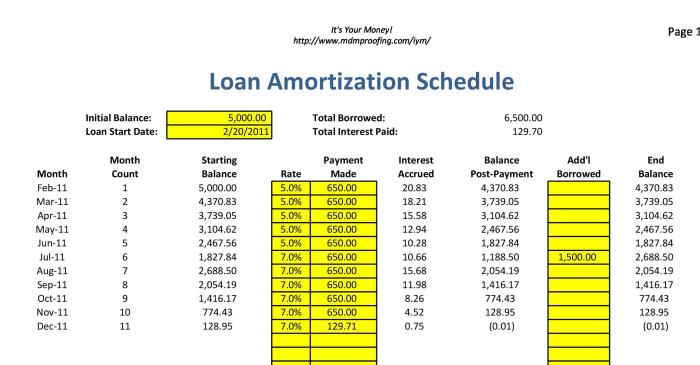
Amortization tables are invaluable tools for understanding and managing student loan debt. By visualizing the repayment schedule, you gain a clear picture of your financial obligations, enabling more informed decisions and proactive debt management strategies. This section explores practical applications, highlights the importance of understanding your schedule, and details the consequences of defaulting, along with effective debt management tips.
Informed Decision-Making with Amortization Tables
An amortization table allows you to compare different repayment plans. For example, you can input different interest rates and loan terms to see how much total interest you’ll pay and the length of your repayment period. Consider a scenario where you have a $30,000 loan. Using an amortization table, you could compare a standard 10-year repayment plan versus a 15-year plan. The 10-year plan will have higher monthly payments but significantly lower total interest paid over the life of the loan compared to the 15-year plan. This comparison helps determine which plan best aligns with your budget and long-term financial goals. Furthermore, you can explore the impact of making extra payments, observing how this accelerates debt reduction and minimizes total interest.
Avoiding Financial Difficulties Through Amortization Schedule Understanding
Understanding your amortization schedule is crucial for avoiding financial hardship. By tracking your payments and projected balance, you can proactively address potential issues. For instance, unexpected job loss or reduced income can be anticipated and mitigated by exploring options like income-driven repayment plans or deferment. Regularly reviewing your amortization table helps you stay on track and identify potential problems early. Ignoring your schedule can lead to missed payments, accumulating late fees, and negatively impacting your credit score. Proactive monitoring, coupled with a well-defined budget, ensures you stay ahead of potential financial difficulties.
Consequences of Student Loan Default
Defaulting on student loans has severe repercussions. It results in damaged credit scores, making it difficult to obtain loans, rent an apartment, or even secure certain jobs. Wage garnishment is a common consequence, where a portion of your earnings is directly seized to repay the debt. Furthermore, tax refunds can be withheld, and your eligibility for government benefits might be affected. In some cases, lawsuits and collection agency involvement can add to the financial burden. The long-term impact of defaulting extends far beyond the immediate financial penalties, significantly hindering future financial opportunities. For example, a default can remain on your credit report for seven years, affecting your ability to secure a mortgage or auto loan for an extended period.
Effective Student Loan Debt Management
Effective student loan management involves proactive strategies. Creating a realistic budget that prioritizes loan payments is paramount. Exploring different repayment options, such as income-driven repayment plans, can adjust monthly payments based on your income and family size. Consolidating multiple loans into a single loan can simplify repayment and potentially lower interest rates. Additionally, making extra payments whenever possible significantly reduces the total interest paid and shortens the repayment period. Regularly reviewing your amortization table and adjusting your repayment strategy as needed ensures you stay on track and effectively manage your student loan debt. Seeking professional financial advice can provide personalized guidance and support in navigating the complexities of student loan repayment.
Ultimate Conclusion
Mastering the art of creating and interpreting a student loan amortization table in Excel is a significant step towards responsible debt management. By understanding the interplay of interest rates, loan terms, and payment amounts, you gain valuable insights into your repayment journey. This empowers you to proactively manage your debt, explore different repayment strategies, and ultimately achieve financial peace of mind. Remember, proactive planning and informed decision-making are crucial for successfully navigating the complexities of student loan repayment.
General Inquiries
What happens if I make extra payments on my student loan?
Extra payments reduce your principal balance faster, leading to lower overall interest paid and a shorter repayment period. Your amortization table will reflect this reduced timeline.
Can I use this Excel template for different types of loans (e.g., car loans, mortgages)?
While the principles remain the same, you’ll need to adjust the input values (loan amount, interest rate, loan term) to accurately reflect the specifics of your different loan.
What if my interest rate changes during the loan term?
You can adjust your Excel amortization table to reflect a new interest rate. This will recalculate the remaining payments and the total interest paid. You’ll need to update the interest rate cell in your spreadsheet.
Where can I find pre-made student loan amortization templates?
Many websites offer free downloadable templates. However, ensure the template’s formulas are accurate before using it with your loan information.
